| 大会 | クラス | 選手 | 成績 |
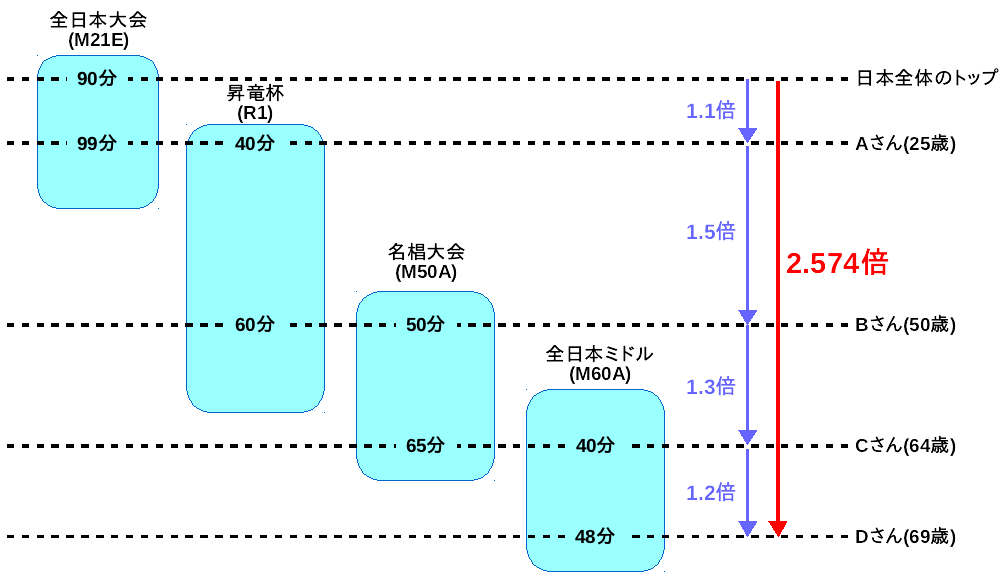
| 全日本大会 | M21E | 優勝者 | 90分 |
| Aさん | 99分 | ||
| 昇竜杯 | R1 | Aさん | 40分 |
| Bさん | 60分 | ||
| 名椙大会 | M50A | Bさん | 50分 |
| Cさん | 65分 | ||
| 全日本ミドル | M60A | Cさん | 40分 |
| Dさん | 48分 |
|
<class name="M21A"
length="4200" climb="230"
controls="12" course="1"
filename="1"> <runner name="細川 知希" id="208289" ecard="208289" club="OLCルーパー" start="11:03:00" result="0:42:26" rank="1" sex="m"> |
|
|
|
|
|
|
|
|
|
|
| イベント | ポイント | 重み | ポイント×重み | ランキングに使用 |
| 大会1 | 95 | 1.0 | 95 | ○ |
| 練習会1 | 90 | 0.9 | 81 | ○ |
| 大会2 | 85 | 1.0 | 85 | ○ |
| 大会3 | 70 | 1.1 | 77 | ○ |
| 練習会2 | 80 | 0.9 | 72 | |
| 大会4 | 65 | 1.0 | 65 | |
| 練習会3 | 60 | 0.9 | 54 |
| 「ポイント×重み」の高い順 | Gさん | Hさん | ||
| ポイント | 重み | ポイント | 重み | |
| 1番目 | 90 | 1.0 | 90 | 0.9 |
| 2番目 | 80 | 1.0 | 80 | 0.9 |
| 3番目 | 70 | 1.0 | 70 | 0.9 |
| 4番目 | 60 | 1.0 | 60 | 0.9 |
|
| 「ポイント×重み」の高い順 | Iさん | Jさん | ||||
| ポイント | 重み | ポイント×重み | ポイント | 重み | ポイント×重み | |
| 1番目 | 90 | 1.1 | 99 | 95 | 1.0 | 95 |
| 2番目 | 80 | 1.1 | 88 | 90 | 1.0 | 90 |
| 3番目 | 85 | 1.0 | 85 | 85 | 1.0 | 80 |
|
|
|
|
| イベント | ポイント | 重み | ポイント×重み |
| 大会1 | 80 | 1.1 | 88 |
| 練習会1(コースa) | 90 | 0.9 | 81 |
| 大会2 | 75 | 1.0 | 75 |
| 練習会2 | 80 | 0.9 | 72 |
| 大会3 | 70 | 1.0 | 70 |
| 練習会1(コースb) | 70 | 0.9 | 63 |
| 大会4 | 55 | 1.0 | 55 |
| 練習会3 | 20 | 0.9 | 18 |
| イベント | ポイント | 重み | ポイント×重み |
| 大会1 | 80 | 1.1 | 88 |
| 大会2 | 75 | 1.0 | 75 |
| 練習会2 | 80 | 0.9 | 72 |
| 大会3 | 70 | 1.0 | 70 |
| 練習会1(コースa) | 75 | 0.9 | 67.5 |
| 練習会1(コースb) | 70 | 0.9 | 63 |
| 大会4 | 55 | 1.0 | 55 |
| 練習会3 | 20 | 0.9 | 18 |
| イベント | ポイント | 重み | ポイント×重み |
| 大会1 | 80 | 1.1 | 88 |
| 大会2 | 75 | 1.0 | 75 |
| 練習会2 | 80 | 0.9 | 72 |
| 練習会1(コースa,bの平均) | 80 | 0.9 | 72 |
| 大会3 | 70 | 1.0 | 70 |
| 大会4 | 55 | 1.0 | 55 |
| 練習会3 | 20 | 0.9 | 18 |
|
|